본 글은 ‘파이썬 알고리즘 인터뷰’ 교재를 참고한 글임
해시 테이블
해시 테이블 또는 해시 맵은 키를 값에 매핑할 수 있는 구조인 연관 배열 추상 자료형(ADT)을 구현하는 자료 구조.
대부분의 연산이 분할 상황 분석에 따른 시간 복잡도가 O(1).
덕분에 데이터 양에 관계 없이 빠른 성능을 기대할 수 있다.
해시
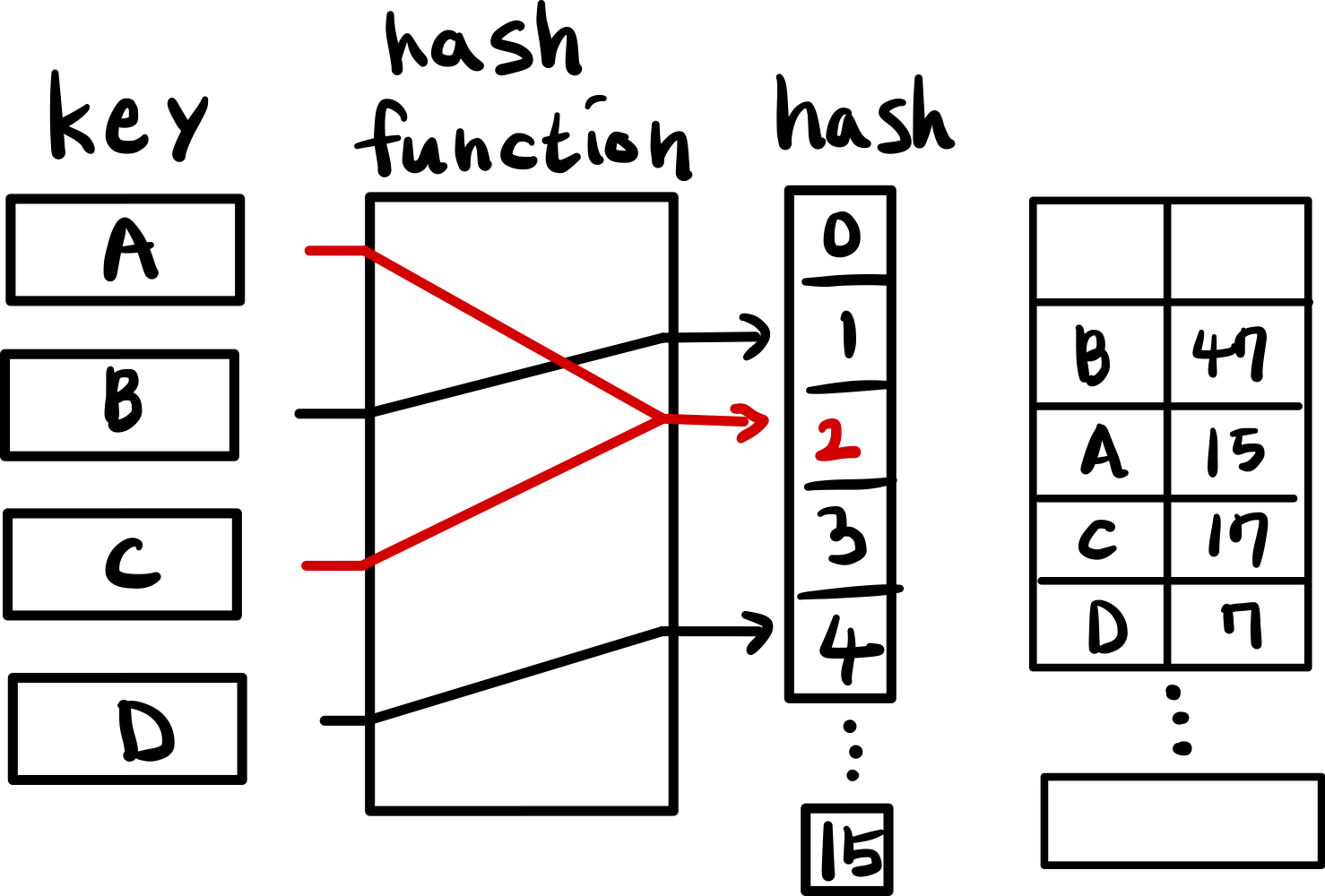
해시 함수란 임의 크기 데이터를 고정 크기 값으로 매핑하는 데 사용할 수 있는 함수로 해시 테이블의 핵심은 해시 함수.
예를 들어, 입력값이 ABC, 1324BC, AF32B 일 때 화살표로 표시한 특정 함수를 통과하면 2바이트의 고정 크기 값으로 매핑. 여기서 화살표 역할을 하는 함수가 해시 함수이다.
ABC -> A1
1324BC -> CB
AF32B -> D5
해시 테이블을 인덱싱하기 위해 해시 함수를 사용하는 것을 해싱(Hashing)이라 하며, 해싱은 정보를 가능한 한 빠르게 저장하고 검색하기 위해 사용하는 중요한 기법 중 하나이다.
용도와 요구사항에 따라 다르게 설계되고 최적화된다.
충돌
성능이 좋은 해시 함수들의 특징으로는 해시 함수 값 충돌의 최소화가 있다.
생일 문제
충돌은 얼마나 많이 발생할지 계산해 보자. 흔한 예로 생일 문제가 있다. 생일의 가짓수는 365개(윤년 제외)이므로 여러 사람이 모였을 때 생일이 같은 2명이 존재할 확률에 대해 생각해보자.
실험에 따르면 23명만 모여도 그 확률이 50%를 넘고 57명이 모이면 그때부터는 99%를 넘어선다.
이처럼 충돌은 생각보다 쉽게 일어나므로 충돌을 최소화 하는 일이 무엇보다 중요하다.
비둘기집 원리
충돌이 왜 일어날 수 밖에 없는지 비둘기집 원리를 통해 설명해 보자.
비둘기집 원리란, n개 아이템을 m개 컨테이너에 넣을 때, n>m이라면 적어도 하나의 컨테이너에는 반드시 2개 이상의 아이템이 들어 있다는 원리를 말한다.
비둘기집 원리에 따라 9개의 공간이 있는 곳에 10개의 아이템이 들어온다면 반드시 1번 이상은 충돌이 발생하게 된다.
좋은 해시 함수라면 충돌을 최소화하여 단 1번의 충돌만 일어나게 하겠지만, 좋지 않은 해시 함수의 경우 심하면 9번을 모두 충돌해서 10개의 공간 중 1개밖에 사용하지 못할 수도 있다.
여러 번 충돌한다는 것은 그만큼 추가 연산을 필요로 하기 때문에 충돌을 최소화하는 것이 좋다.
로드팩터
해시 테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것
\[load factor = n/k\]로드 팩터 비율에 따라 해시 함수를 재작성해야 될지 또는 테이블의 크기를 조정해야 할지를 결정한다. 또한 이 값은 해시 함수가 키들을 잘 분산해 주는지를 말하는 효율성 측정에도 사용된다.
해시 함수
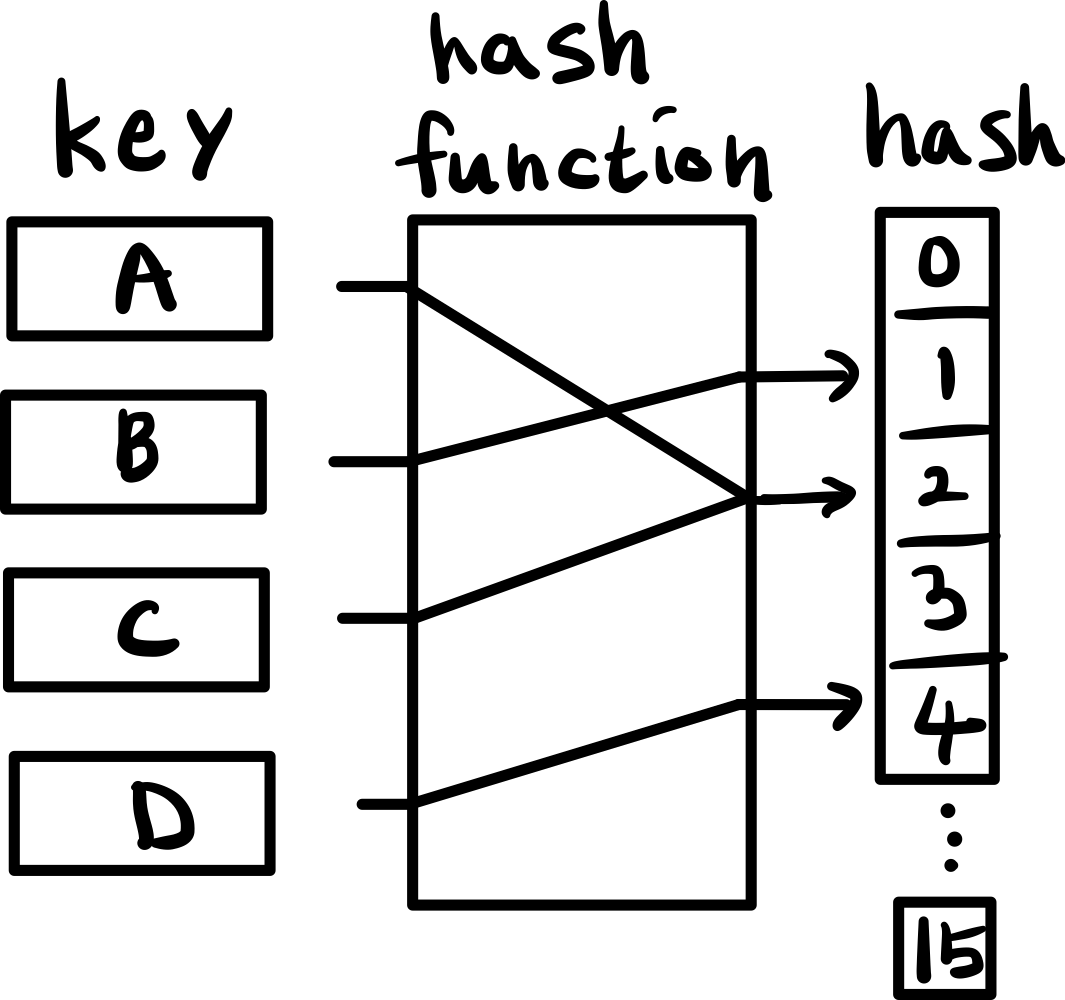
이렇게 해시 테이블을 인덱싱하기 위해 해시 함수를 사용하는 것을 해싱(Hashing)이라고 한다. 해싱에는 다양한 알고리즘이 있으며, 최상의 분포를 제공하는 방법은 데이터에 따라 제각각이다.
가장 단순하면서도 널리 쓰이는 정수형 해싱 기법인 모듈로 연산을 이용한 나눗셈 방식이 있다.
\[h(x) = x\,mod\,m\]h(x)는 입력값 x의 해시 함수를 통해 생성된 결과, m은 해시 테이블의 크기, x는 어떤 간단한 규칙을 통해 만들어낸 충분히 랜덤한 상태의 키의 값이다.
해시 테이블의 충돌 처리 방식
아무리 좋은 해시 함수라도 아래 그림과 같이 충돌은 발생하게 된다.
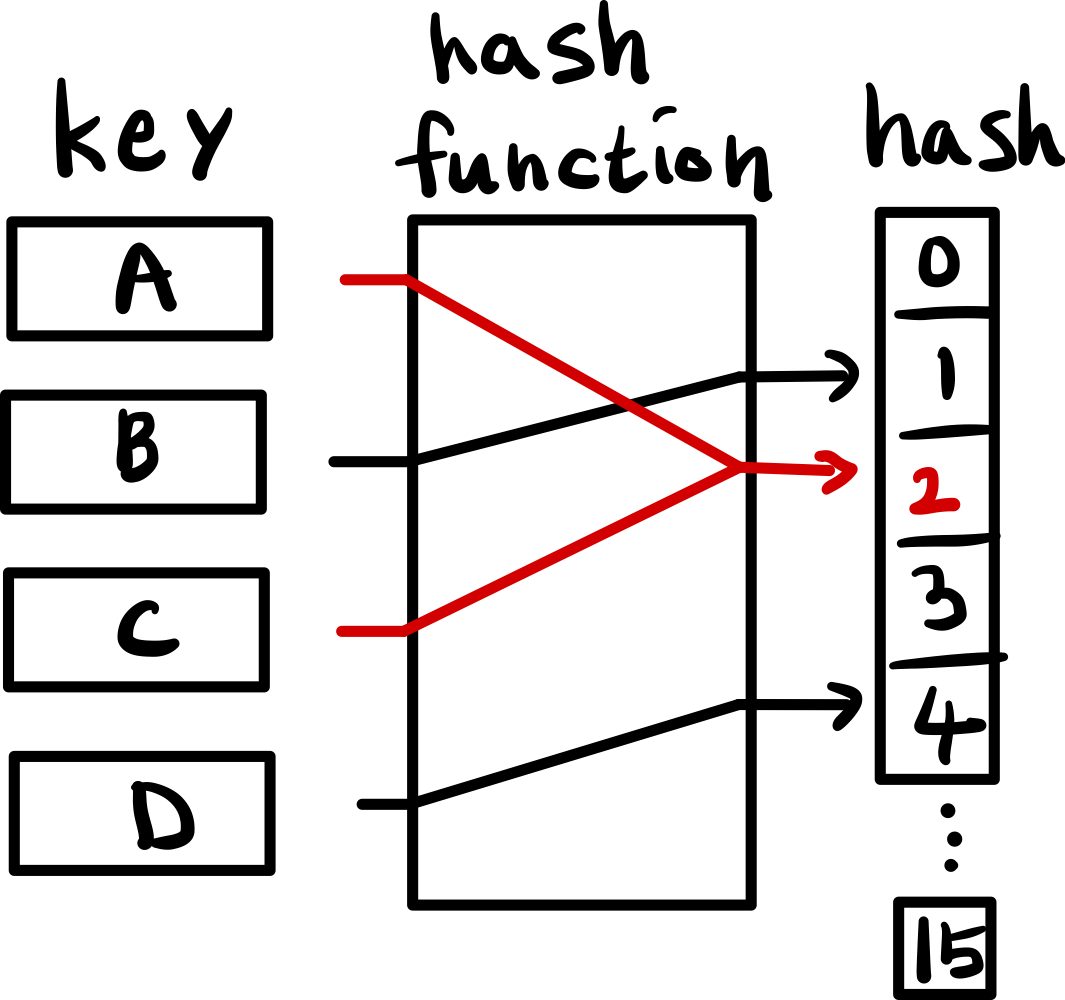
개별 체이닝
개별 체이닝은 충돌 발생 시 연결 리스트로 연결하는 방식이다.
아래 표와 같이 입력값이 있다고 하자. 해시는 키를 해싱한 결과이다.
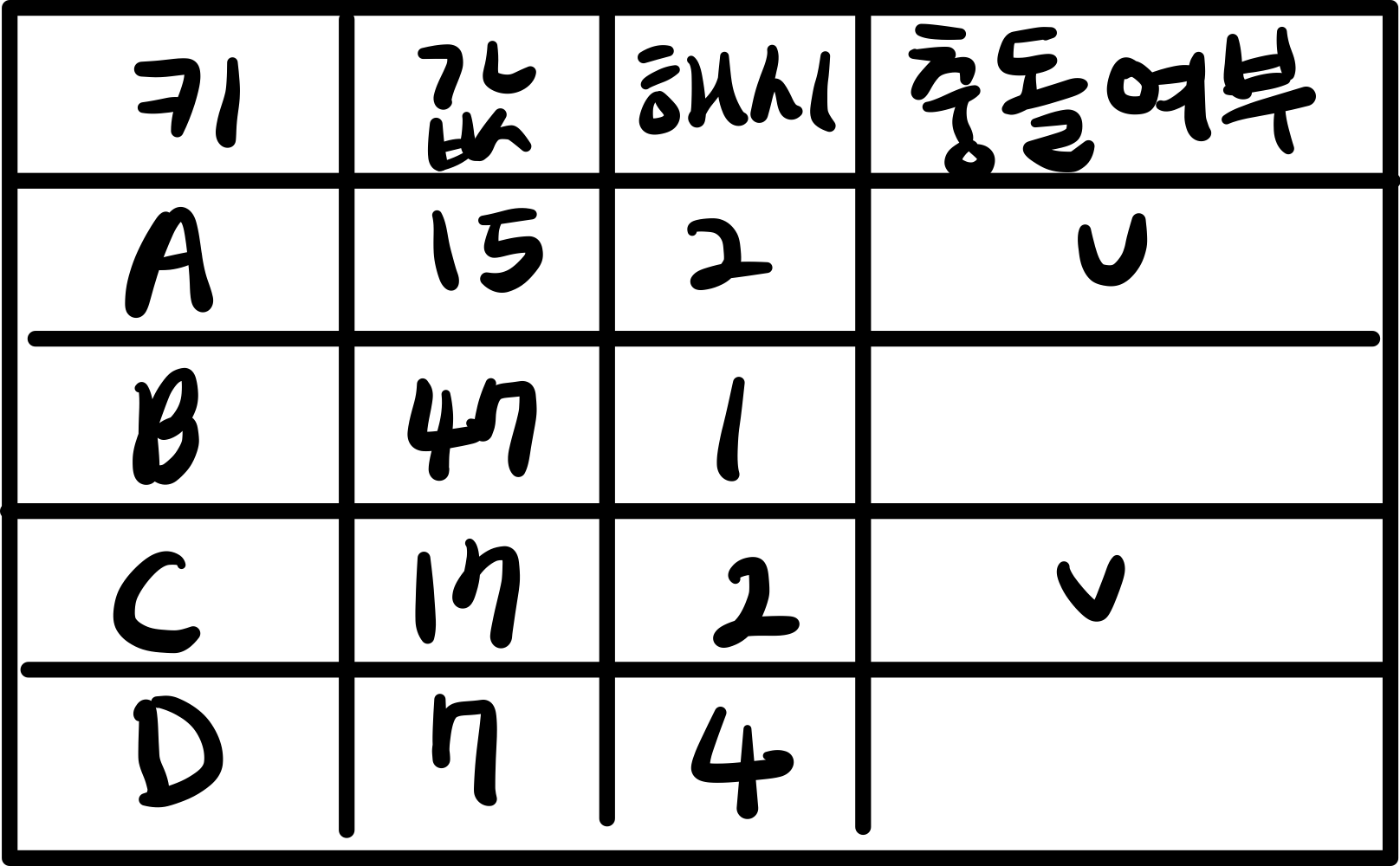
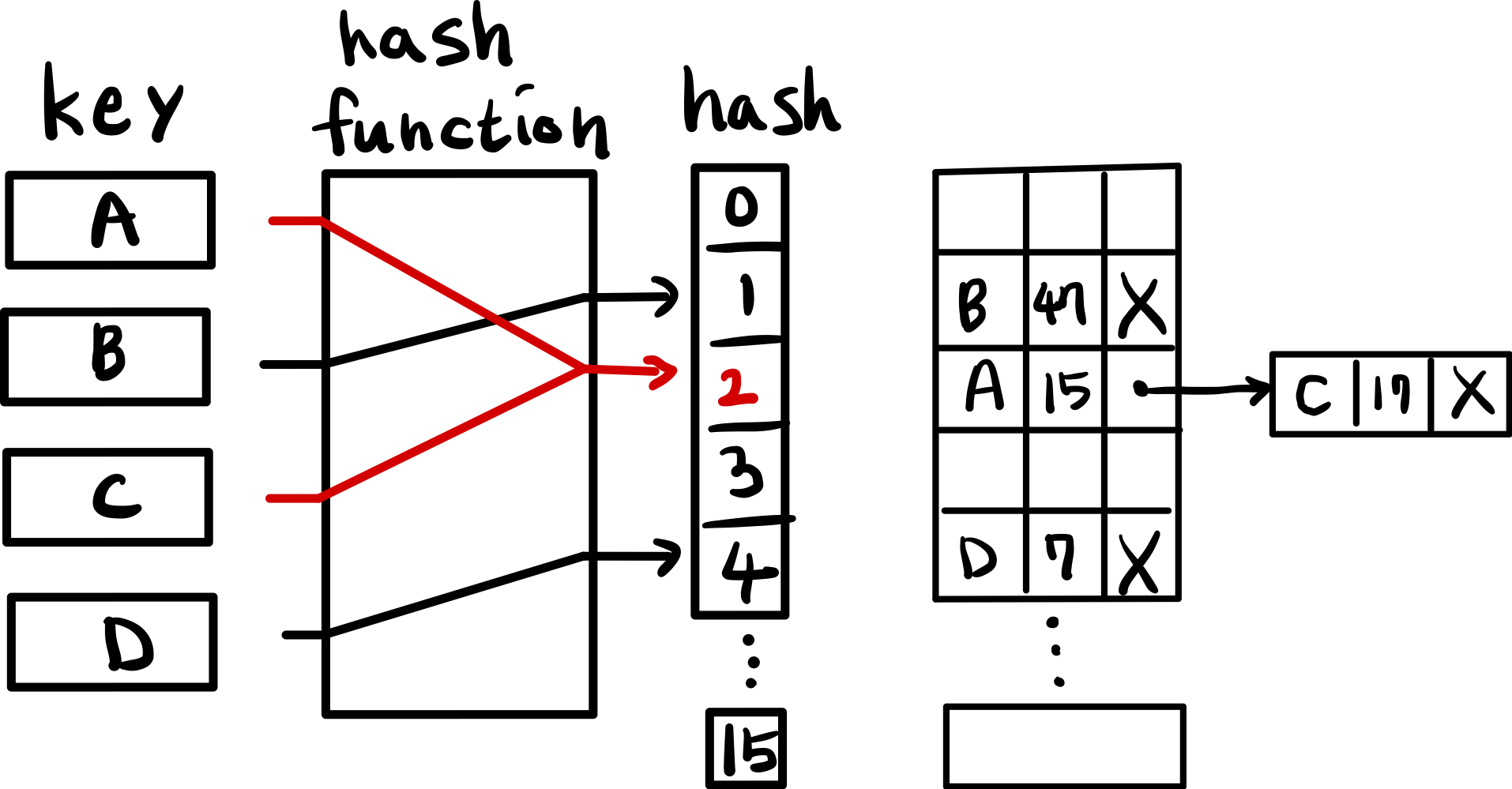
흔히 해시 테이블이라고 하면 바로 이 방식을 말한다.
잘 구현한 경우 대두분의 탐색은 O(1)이지만 최악의 경우, 즉 모든 해시 충돌이 발생했을 시에는 O(n)이 된다. 충돌이 계속 발생하면 연결리스트가 길어지기 때문인 것 같다.
오픈 어드레싱
충돌 발생 시 탐사를 통해 빈 공간을 찾아나서는 방식이다.
무한정 저장할 수 있는 체이닝 방식과 달리 전체 슬롯의 개수 이상은 저장할 수 없다. 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장은 없다.
가장 간단한 방식인 선형 탐사(Linear Probing) 방식은 충돌이 발생할 경우 해당 위치부터 순차적으로 탐사를 하나씩 진행한다. 특정 위치가 선점되어 있으면 바로 그 다음 위치를 확인하는 식이다.
선형 탐사의 문제점으로는 해시 테이블에 저장되는 데이터들이 고르게 분포되지 않고 뭉치는 클러스터링 현상이 있다. 이는 탐사 시간을 오래 걸리게 하며 전체적으로 해싱 효율을 떨어뜨리는 원인이 된다.
오픈 어드레싱 방식은 버킷 사이즈보다 큰 경우에는 삽입할 수 없다. 일정 이상 채워지면, 즉 기준이 되는 로드 팩터 비율을 넘어서게 되면 그로스 팩터(Growth Factor)의 비율에 따라 더 큰 크기의 또 다른 버킷을 생성한 후에 여기에 새롭게 복사하는 리해싱(Rehashing) 작업이 일어난다.
파이썬 해시 테이블 구현 방식
해시 테이블로 구현된 파이썬 자료형은 딕셔너리이다. 파이썬의 해시 테이블에서는 충돌 시 오픈 어드레싱 방식으로 처리한다. 체이닝 시 malloc으로 메모리를 할당하는 오버헤드가 높아 오픈 어드레싱을 택했다고 한다.
연결 리스트를 만들기 위해서는 추가 메모리 할당이 필요하고, 추가 메모리 할당은 상대적으로 느린 작업이라고 한다.
오픈 어드레싱의 한 방식인 선형 탐사 방식은 일반적으로 체이닝에 비해 성능이 더 좋지만 슬롯의 80% 이상이 차게 되면 급격한 성능 저하가 있다.
최근의 루비나 파이썬 같은 최신 언어들은 오픈 어드레싱 방식을 택해 성능을 높이는 대신, 로드 팩터를 작게 잡아 성능 저하 문제를 해결한다.
