(Python) 최단 경로 실전 문제 - 미래 도시

본 글은 “이것이 취업을 위한 코딩 테스트다 with 파이썬” 교재를 참고한 것임

문제

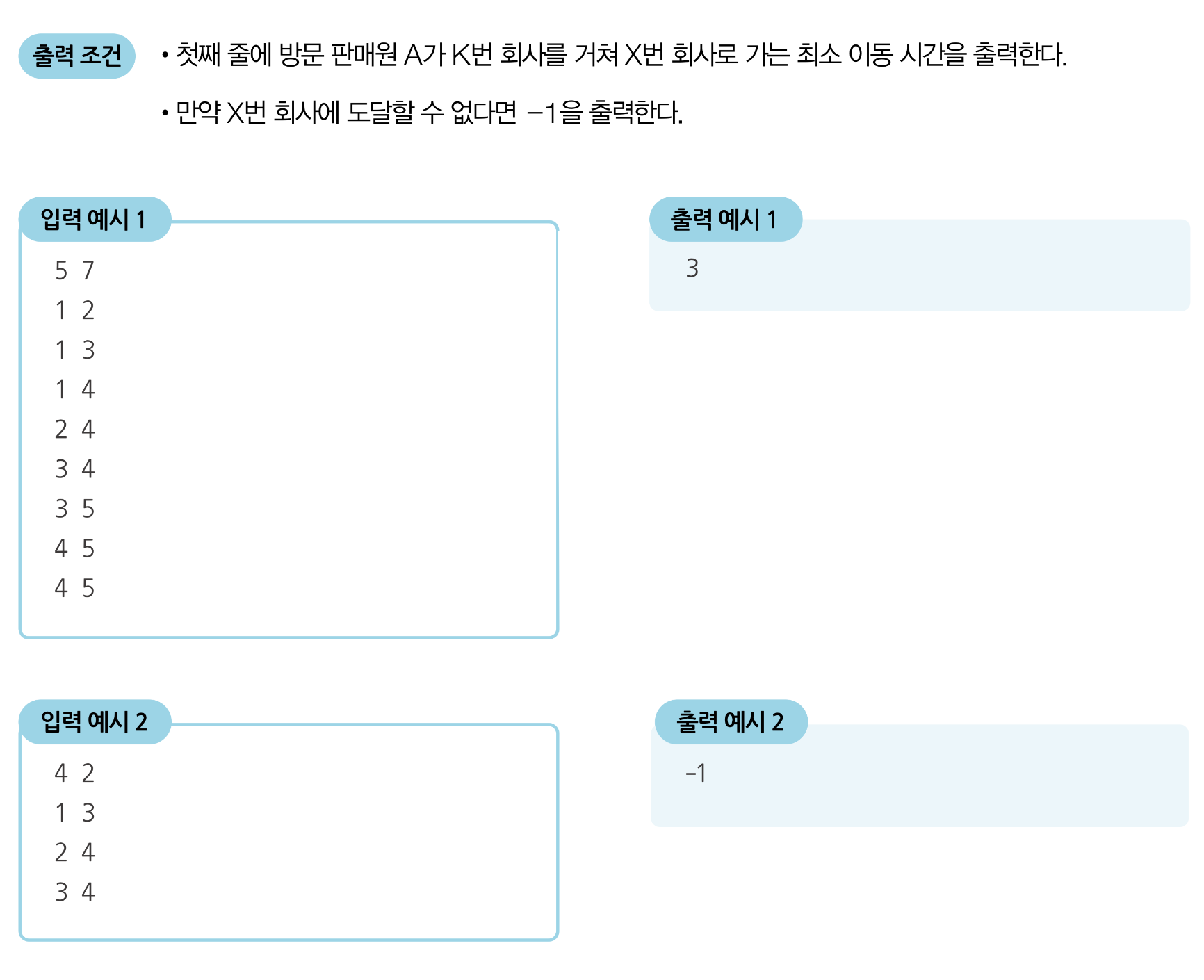
문제 풀이

해당 노드를 거쳐 가는 경우를 고려하며 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우이므로 플로이드 워셜알고리즘을 사용한다. 따라서 2차원 리스트에 최단 거리를 저장한다.

소스코드

INF = int ( 1e9 ) # 무한을 의미하는 값으로 10 억을 설정
# 노드의 개수 및 간선의 개수를 입력받기
n, m = map(int, input().split())
# 2 차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[ INF ] * ( n + 1 ) for _ in range ( n + 1 )]

# 자기 자신에서 자기 자신으로 가는 비용은 0 으로 초기화
for a in range ( 1 , n + 1 ):
    for b in range ( 1 , n + 1 ):
        if a == b :
            graph [ a ][ b ] = 0

# 각 간선에 대한 정보를 입력받아, 그 값으로 초기화
for _ in range ( m ):
    # A 에서 B 로 가는 비용은 1이라고 설정
    a , b = map ( int , input (). split ())
    graph [ a ][ b ] = 1
    graph [ b ][ a ] = 1

# 거쳐갈 노드 k와 최종 목적지 노드 x를 입력받기
k, x = map(int, input().split())

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range ( 1 , n + 1 ):
    for a in range ( 1 , n + 1 ):
        for b in range ( 1 , n + 1 ):
            graph [ a ][ b ] = min ( graph [ a ][ b ], graph [ a ][ k ] + graph [ k ][ b ])

# 수행된 결과를 출력
distance = graph [ 1 ][ k ] + graph [ k ][ x ]

# 도달할 수 없는 경우, - 1 을 출력
if distance >= INF :
    print ("- 1 ") # 도달할 수 있다면, 최단 거리를 출력
else :
    print ( distance )