(Python)[백준][DP] 계단 오르기

2579번: 계단 오르기

문제 풀이

---

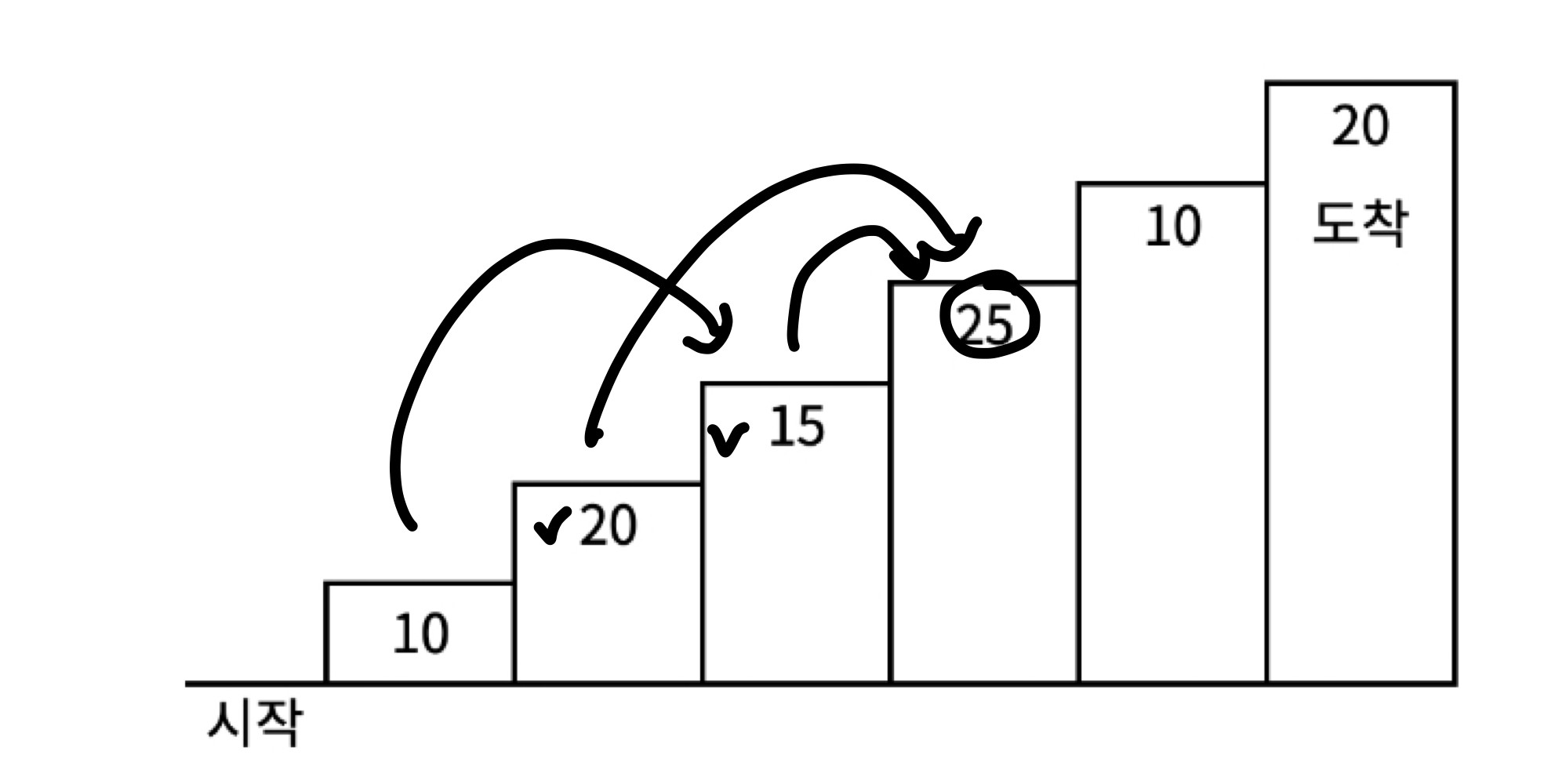
1. dp[3]인 25에 도달하려면 15에서 오거나 20에서 왔을 것이다.
2. 하지만 연속으로 세 개의 계단을 밟는 경우가 안되므로 10-15-25 로 오거나, 20-25로 오는 두 가지 경우의 수가 존재한다.
3. 해당 지점까지 왔을 때의 최대 점수를 dp 테이블에 저장시키면서 진행한다.

첫 소스 코드

# 계단의 수
n = int(input())

# 계단에 쓰여있는 점수
scores = []
for _ in range(n):
    scores.append(int(input()))

# DP 테이블 초기화
dp = [0] * n

# DP 진행
dp[0] = scores[0]
dp[1] = scores[0] + scores[1]
dp[2] = max(scores[0] + scores[2], scores[1] + scores[2])
for i in range(3, n):
    dp[i] = max(dp[i-2] + scores[i], dp[i-3] + scores[i] + scores[i-1])

print(dp[n-1])

런타임 에러가 난다. 알아보니 계단이 1개나 2개인 경우라면 scores, dp 값이 존재하지 않기 때문인 거 같다. 따라서 길이를 처음부터 정해서 배열을 구현한다.

소스 코드

# 계단의 수
n = int(input())

# 계단에 쓰여있는 점수
scores = [0] * 300
for i in range(n):
    scores[i] = int(input())

# DP 테이블 초기화
dp = [0] * 300

# DP 진행
dp[0] = scores[0]
dp[1] = scores[0] + scores[1]
dp[2] = max(scores[0] + scores[2], scores[1] + scores[2])
for i in range(3, n):
    dp[i] = max(dp[i-2] + scores[i], dp[i-3] + scores[i] + scores[i-1])

print(dp[n-1])