풀이
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 높이 h부터 높이 1까지 누적 합을 계산하면 높이 i의 배열 값은 높이 i 이상의 모든 석순의 개수
# 예를 들어, 높이가 6인 동굴에서 높이 5의 개똥벌레가 날아갈 때,
# 높이 5 이상의 석순에 모두 부딪히기 때문에 배열 5의 값이 높이 5의 개똥벌레가 부딪히는 석순의 개수
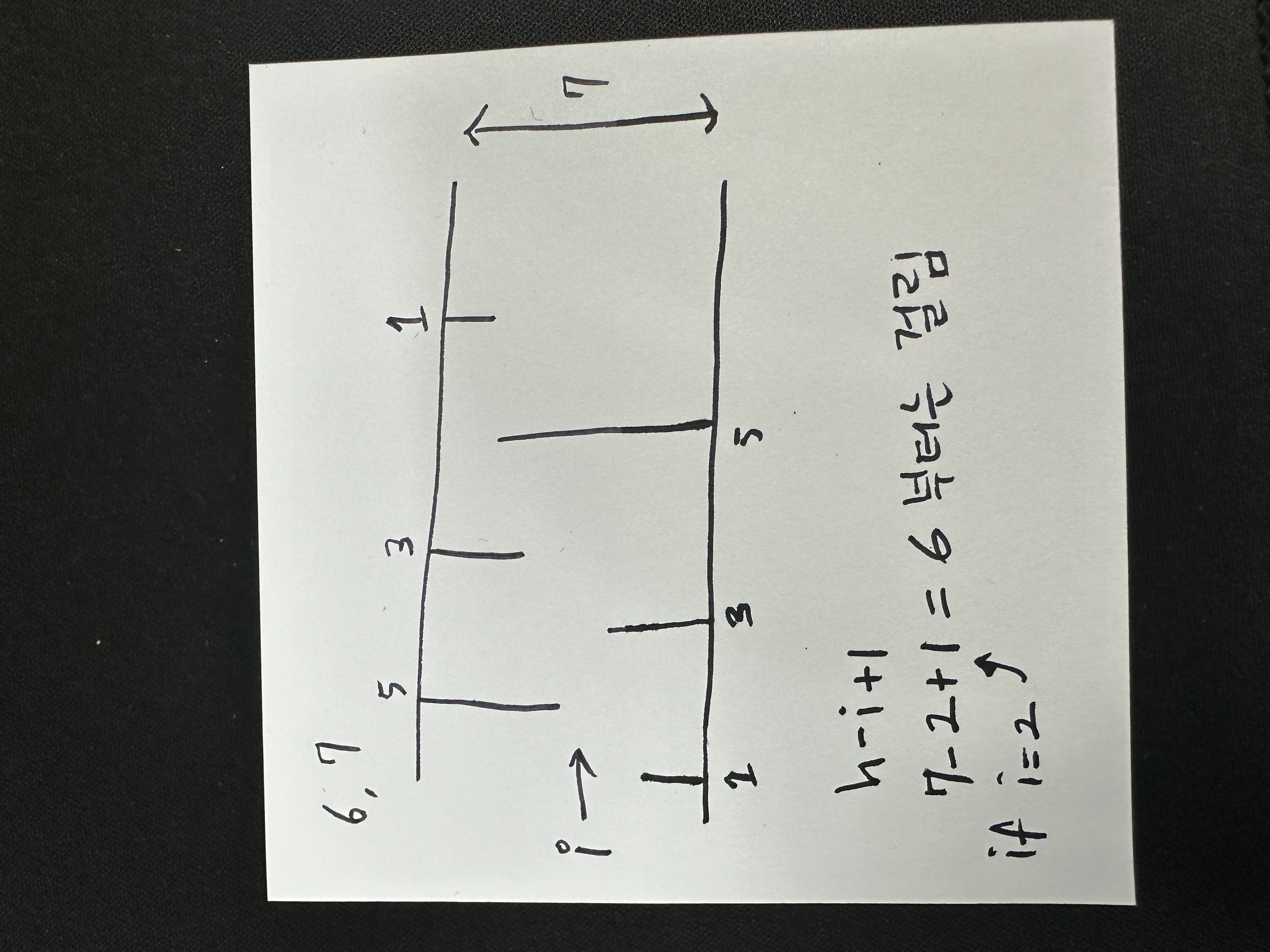
# 마찬가지로 종유석은 위에서부터 내려오기 때문에 h - i + 1의 식을 이용
# 왜냐하면, 높이 6의 동굴에서 높이 2짜리 종유석은 높이 4 위로의 개똥벌레가 모두 부딪히기 때문
# 장애물의 개수와 전체 높이
n, h = map(int, input().split())
# 석순 정보 저장
down = [0] * (h+1)
# 종유석 정보 저장
up = [0] * (h+1)
for i in range(n):
height = int(input())
if (i % 2 == 0):
# 석순의 높이에 따라 1 증가
down[height] += 1
else:
# 종유석의 높이에 따라 1 증가
up[height] += 1
# 인덱스를 역순으로 누적합을 계산
for i in range(h-1, 0, -1): # h = 6 , 5 , 4
down[i] += down[i+1]
up[i] += up[i+1]
# 최소로 잘리는 장애물의 개수
min_count = n
# 동일한 개수로 잘리는 높이의 수
same_height = 0
# 전체 높이 i 기준, 높이에 따라 잘리는 석순과 종유석의 개수 파악
for i in range(1, h+1):
# 현재까지 최소로 잘린 개수보다 현재 높이에서 더 적은 수로 잘리는 경우
if (min_count > down[i] + up[h - i + 1]):
min_count = down[i] + up[h - i + 1]
same_height = 1
# 현재 높이에서 잘린 개수가 현재까지 최소로 잘린 개수와 동일하다면
elif (min_count == down[i] + up[h - i + 1]):
same_height += 1
print(min_count, same_height)
